La Conjetura de Poincaré fue una de las hipótesis más importantes de la Topología, y dejó de ser conjetura para convertirse en teorema tras su demostración por el ruso Perelman en fecha tan reciente como 2006. El teorema afirma que «La esfera tridimensional (también llamada 3-esfera o hiperesfera) es la única variedad compacta de dimensión 3 en la que todo lazo o círculo cerrado se puede deformar (transformar) en un punto». Este último enunciado es equivalente a decir que «Sólo hay una variedad cerrada y simplemente conexa de dimensión 3, la esfera tridimensional», o bien, «Cualquier variedad compacta simplemente conexa de dimensión 3 sin frontera es homeomorfa a la esfera». Compacta significa que la variedad no es ilimitada (en IRⁿ compacto significa cerrado y acotado). Coloquialmente, una superficie es simplemente conexa cuando no tiene agujeros. Más rigurosamente, cuando cualquier curva cerrada contenida en ella puede deformarse hasta convertirse en un punto. Por ejemplo lo es la esfera pero no el toro.

Vamos a explicar esto. La 1-esfera sería una circunferencia (x₁²+x₂²=r²) y la 2-esfera una esfera usual (x₁²+x₂²+x₃²=r²). Lo mejor es empezar viendo que la conjetura es muy intuitiva en este último caso de dimensión 2. La superficie de un balón de fútbol, por ejemplo, es casi un ejemplo de variedad de dimensión 2, una 2-esfera; lo podemos manipular como queramos, dándole diferentes formas, pero sin romperlo, y seguirá siendo una 2-esfera. Pues bien, el criterio para comprobar si una variedad es una 2-esfera es muy sencillo: imagínese una goma elástica tremendamente deformable apoyada sobre la superficie del balón; si la goma se puede comprimir (sin salirse de la superficie) hasta ocupar un solo punto, y esto en cualquier parte de la superficie, el balón es una 2-esfera, y se dice que es simplemente conexa:

NOTA: La 2-esfera es una superficie de dimensión 2 -es como la cáscara de una naranja (sólo la cáscara, sin incluir el interior)-. También lo es el toro, esto es, la superficie de un donut:

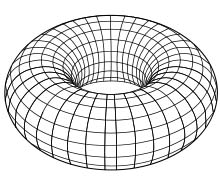
Estas superficies son bidimensionales porque (al menos localmente) podemos describir en qué punto de la superficie estamos dando dos números. Pensemos en la superficie de la Tierra, donde sólo necesitamos la latitud y la longitud…

El problema es que ¡no podemos ver la 3-esfera! porque no vive en el espacio tridimensional (su ecuación sería (x₁²+x₂²+x₃²+x₄²=r²), al igual que la 2-esfera no vive en el plano. ¡Ojo! Es un error pensar que la 3-esfera es una bola rellena, es decir el cuerpo sólido que encierra la 2-esfera. Esa es una intuición infundada.

 

Teorema (Clasificación de superficies): Las superficies cerradas de dimensión 2 son las siguientes: la esfera y los toros de género finito cualquiera (El género de una figura es el número de agujeros que tiene).

 

Cuando decimos que una determinada superficie es una esfera, entendemos que es homeomorfa a una esfera. Por ejemplo, que podemos deformar la cucharilla de la siguiente figura en una esfera:

  

Un homeomorfismo, en topología, es toda transformación continua que conserva la forma. Por ejemplo, una esfera y una cucharilla son homeomorfas, y también una taza y un donut; en cambio, una taza y una esfera no lo son.

El problema de clasificar las variedades en el espacio usando como criterio de clasificación el concepto de homeomorfismo fue resuelto en el siglo XIX. Como hemos dicho arriba, la esfera es una variedad de dimensión 2 (cada trozo pequeño de la esfera es un pequeño trozo de plano ligeramente deformado), cerrada y simplemente conexa, y se estableció que toda variedad de dimensión 2, cerrada y simplemente conexa es homeomorfa a la esfera. Dicho de otro modo: sólo hay una variedad (homeomórfica) de dimensión n=2, cerrada y simplemente conexa, y se trata de la esfera (y sus homeomorfos). En topología, dos figuras son homeomorfas (es decir, equivalentes) si una se puede obtener de la otra doblando, estirando, encogiendo, retorciendo... pero siempre sin romper nada ni colapsar agujeros. Es decir, para un topólogo una taza es igual a un toro (un donut):

Se sabe que todas las superficies de dimensión 2 son topológicamente equivalentes (la palabra adecuada es homeomorfas) a la 2-esfera, o al toro, o al toro de 2 agujeros, o al de 3, etc. 

La motivación de Poincaré fue seguramente por analogía con la dimensión 2, donde todo se entendía. Estaba buscando una propiedad sencilla que caracterizara el espacio tridimensional más simple, la 3-esfera. ¿Qué propiedad era esa? Volvamos a las superficies:

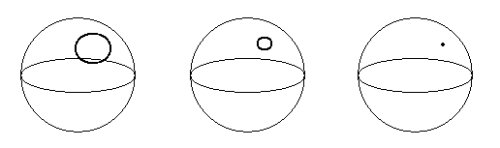
Si dibujamos cualquier lazo (una curva cerrada simple, esto es, que no se corta a sí misma) en la superficie de la esfera, podemos “encogerlo” hasta convertirlo en un punto:

Pero en un toro no siempre podemos hacer esto; por ejemplo, los dos siguientes lazos no se pueden encoger hasta un punto de manera continua:

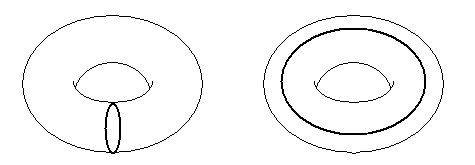
Y en el toro de género 2 (un flotador en forma de 8) también podemos construir estos mismos lazos, que no se pueden encoger hasta un punto. Y en el de género 3, etc.

Y de hecho se sabe que esto ocurre para cualquier superficie que no sea la esfera. Es decir, la propiedad de que todo lazo puede encogerse (continuamente) hasta un punto, caracteriza a la 2-esfera.

Igual que para la 2-esfera, todo lazo en la 3-esfera puede contraerse a un punto.

¿Qué pasa con el recíproco? El recíproco es la conjetura de Poincaré: “Si un espacio tridimensional tiene la propiedad de que todo lazo en ese espacio puede encogerse a un punto, entonces ese espacio es topológicamente equivalente a la 3-esfera”.

 En efecto, en 1904 el matemático francés Henri Poincaré (1854-1912) (figura izquierda) conjeturó que el resultado obtenido para la esfera n=2 del espacio de dimensión 3 tenía un análogo para la esfera n=3 del espacio de dimensión 4. En otras palabras, en el espacio de dimensión 4, toda variedad de dimensión n=3, cerrada y simplemente conexa, sería homeomorfa a la esfera de dimensión n=3. Pero Poincaré no consiguió probar su conjetura. Tampoco ninguno de sus contemporáneos ni sucesores. Con el tiempo, la conjetura de Poincaré cobró interés hasta convertirse en el problema abierto más notable de la Topología geométrica, con destacables implicaciones para la Física. Más aún, llegó a convertirse en uno de los problemas sin resolver más importantes de la Matemática.

Para dimensión dos ya fue demostrada en el siglo XIX. Para n=5, hubo de esperar hasta 1961, cuando lo hizo Erik Christopher Zeeman. Ese mismo año, Stephen Smale (1930-  ) lo consiguió para n mayor o igual que 7 y, en 1962, John R. Stallings para el caso n=6. Los casos n=3 y n=4 se resistían y hubo que esperar a 1986 cuando, en lo que se consideró una hazaña matemática del estadounidense Michael Hartley Freedman, se consiguió demostrar el caso n=4. El problema es que, resuelto con éxito para todas las demás dimensiones, el caso original n=3, planteado por  Poincaré, se resistía denodadamente a cualquier demostración matemática.

Su demostración fue considerada uno de los Siete Problemas del Milenio propuestos por el Clay Mathematics Institute en 2000, ofreciendo 1.000.000 $ por la solución de cada uno. Finalmente, el excéntrico matemático ruso Grigori Perelman (figura derecha) hizo pública su demostración. Justamente por resolver este problema, Perelman recibió en 2006 la medalla Fields, considerada el Nobel de las matemáticas. Otro premio que también rechazó.

La historia de este hallazgo ha sido controvertida: Perelman anunció haberlo demostrado en 2002 a través de dos publicaciones en Internet. En junio de 2006 los matemáticos chinos Zhu Xiping y Cao  Huaidong anunciaron la demostración completa, basándose en los trabajos preliminares de Perelman  (éstos sí publicados en revistas especializadas), lo que, una vez realizada su validación por la comunidad matemática, daría fin a la clasificación completa de las estructuras topológicas de dimensión 3. Sin embargo, una gran parte de la comunidad matemática piensa que la demostración corresponde a Perelman y considera el trabajo de los matemáticos chinos como un plagio. La Academia China de Ciencias, en defensa de Zhu Xiping y Cao Huaidong, afirmó que el ruso estableció las líneas generales para probar la conjetura, pero no dijo específicamente cómo resolver el enigma. Finalmente, se reconoció el trabajo de Perelman cuando se le otorgó la Medalla Fields en el marco del XXV Congreso Internacional de Matemáticos celebrado en Madrid en agosto de 2006, la cual rechazó. En declaraciones a un semanario estadounidense Perelman aseguró no querer ser una mascota en el mundo de las matemáticas, estimando que no necesita otro reconocimiento sobre la validez de su trabajo.

 

Fuentes:   «Ideas fugaces. Teoremas eternos». Navarro, Joaquín. Ed. RBA, 2010

http://es.wikipedia.org