Página actualizada por última vez el 19 Agosto, 2021
LA CUADRATURA DEL CÍRCULO
Desde tiempos inmemoriales los matemáticos griegos buscaron infructuosamente la cuadratura del círculo, es decir, obtener, a base únicamente de regla y compás, un rectángulo de área igual a la de un círculo dado.
La
resolución de este problema trató de abordarse repetidas veces, sin éxito,
desde la antigüedad clásica hasta el siglo XIX. En 1882, el matemático alemán Ferdinand Lindemann probó que
π es un número trascendente, lo que implica que es imposible cuadrar el círculo
usando regla y compás.
Otras
famosas construcciones imposibles con regla y compás son la duplicación del
cubo y la trisección del ángulo.
Hablando
en sentido figurado, se dice de algo que es la "cuadratura del
círculo" cuando representa un problema muy difícil o imposible de
resolver.
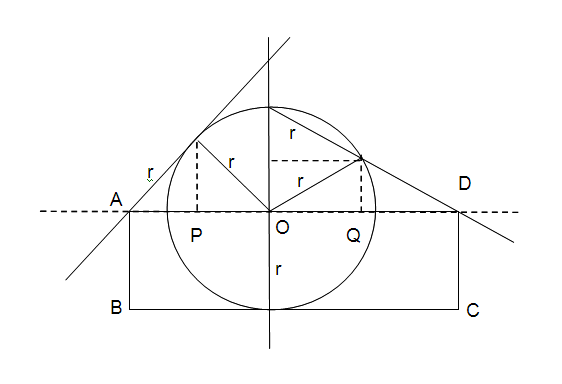
Uno de los múltiples intentos puede verse en la figura siguiente:
Puede demostrarse fácilmente que el área del
rectángulo ABCD es
(Ayuda: Hallar, por Pitágoras,
y
, y plantear semejanza de triángulos)
Como
puede comprobarse que 
, con un error del 0,15%, concluiríamos que ¡el área del
rectángulo es prácticamente igual al área del círculo! (con un error del
0,15%).
(Fuente:
Karl R. Popper, La sociedad abierta y sus
enemigos, cap. VI)
